이대호라면 가능할 4할 타율 '조건 3가지'

압도적인 타율로 이 부문 리그 1위 질주

출루율 높아 4할 타율 가능성 충분히 존재

4할 타율을 유지 중인 이대호. ⓒ 데일리안 DB

돌아온 ‘빅보이’ 이대호가 차원이 다른 타격으로 KBO리그를 지배하고 있다.

18경기 출전한 이대호는 타율 0.438 5홈런 13타점으로 매 경기 무시할 수 없는 존재감을 드러내고 있다. 타율은 2위 최형우(KIA, 0.377)과 무려 6푼 이상 차이 나는 1위이며, 홈런은 공동 2위, 타점은 공동 8위에 랭크되어 있다.

시즌이 시작된 지 한 달도 되지 않았지만 이대호이기에 기대되는 기록이 있다. 바로 KBO리그 역사상 단 한 번만 나왔던 4할 타율이다.

4할 타율은 현대 야구에서 사실상 불가능한 기록으로 여겨진다. 100년 넘는 역사를 자랑하는 메이저리그에서는 4할 타율이 42번이나 나왔지만 마지막 기록자는 70년도 더 된 1941년 보스턴 레드삭스의 테드 윌리엄스(0.406)이다. 마찬가지로 80년 된 일본프로야구에서는 아직 4할 타자가 탄생되지 않았다.

KBO리그에서는 출범 첫 해인 1982년 MBC의 백인천(0.412)이 유일한 달성자다. 백인천 이후 타율 4할에 근접했던 선수는 ‘안타제조기’ 장효조와 ‘바람의 아들’ 이종범이다.

장효조는 삼성 시절이던 1987년, 8월 중순까지 4할의 타율을 유지하고 있었지만 기록에 대한 중압감과 체력적인 문제로 타율의 하락을 막지 못했다. 결국 4할에 조금 모자란 타율 0.387로 아쉽게 시즌을 마쳤고, 이는 역대 한 시즌 타율 3위의 기록으로 남아있다.

그라운드에 거센 바람을 몰고 온 이종범의 1994시즌은 프로야구 역사에 길이 남는 몬스터시즌으로 불린다. 당시 이종범은 장효조보다 이틀이나 더 4할을 유지하고 있었다. 하지만 이종범도 컨디션 조절에 실패하며 타율 0.393에서 여정을 마쳤다.

타율 4할이 어려운 이유는 홈런, 타점 등과 같은 누적기록과 달리 비율 기록이라 플러스, 마이너스가 있기 때문이다. 간단한 예로 한 타자가 한 경기에 5번 타석에 들어선다고 가정했을 때 멀티 히트가 아니라면 타율이 떨어지는 구조다. 따라서 10번 중 3번만 쳐도 성공이라는 야구에서 ‘타율 4할’은 꿈의 기록으로 불린다.

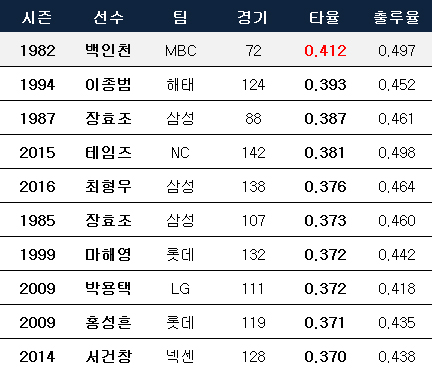KBO리그 한 시즌 타율 순위. ⓒ 데일리안 스포츠

그렇다고 달성 가능성이 아주 없는 것은 아니다. 많은 전문가들은 세 가지 조건이 충족될 경우 타율 4할에 근접할 수 있다고 입을 모은다.

먼저 잘 쳐야 한다. 안타를 만들어야 타율이 올라가기 때문이다. 하지만 타율 3할도 쉽지 않은 게 야구다. 또한 6개월간의 길고 긴 페넌트레이스에서 시즌 내내 타격감을 유지하기도 만만치 않다.

일단 올려놓은 타율을 떨어뜨리지 않는 것도 중요하다. 야구는 타자가 방망이를 내미는 순간 아웃될 확률이 높기 때문이다. 따라서 타석은 늘어나되 타석수 증가를 막는 방법은 바로 볼넷이다.

볼넷을 얻으면 타석수가 늘면서 타율은 그대로 유지할 수 있다. 테드 윌리엄스는 1941시즌 안타 개수(185개)가 리그 5위에 불과했지만 볼넷이 무려 147개에 달했다. 불확실성에 승부를 걸기 보다는 타율을 유지하는 방법이 윌리엄스의 4할을 가능케 한 이유다.

타자의 타순도 중요하다. 아무래도 1~2번에 위치한 테이블세터진은 타석에 많이 들어서기 때문에 타율 관리가 어려워질 수밖에 없다. 1994년 이종범이 4할에 실패한 이유도 너무 많은 타석에 들어섰기 때문으로 풀이된다.

이 세 가지 조건을 모두 충족하는 이가 바로 이대호다. 이대호는 안타생산력도 뛰어난데다 사사구 역시 안타 수 절반에 해당하는 13개를 얻어냈다. 출루율(0.532)이 타율보다 약 1할 높고, 중심 타선에 위치해있어 최적의 조건을 갖추고 있다. 남은 5개월간 컨디션 유지만 잘하면 꿈의 4할에 도전장을 내밀 수 있다.